Deep Learning In Borel Measure

DOI:
https://doi.org/10.54060/a2zjournals.jase.102Keywords:
Deep learning, Machine learning, Convolutional arithmetic circuits, Formalization, TensorsAbstract
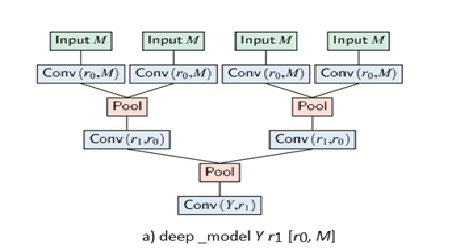
Deep learning has had a profound impact on computer science in recent years, with applications to image recognition, language processing, bioinformatics, and more. Recently, Cohen et al. provided theoretical evidence for the superiority of deep learning over shallow learning. We formalized their mathematical proof using Isabelle/HOL. The Isabelle development simplifies and generalizes the original proof, while working around the limitations of the HOL type system. To support the formalization, we developed reusable libraries of formalized mathematics, including results about the matrix rank, the Borel measure, and multivariate polynomials as well as a library for tensor analysis.
Downloads
References
B. W. Bader, T. G. Kolda, “Algorithm 862: MATLAB tensor classes for fast algorithm prototyping,” ACM Trans. Math. Softw. vol. 32, no. 4, pp. 635–653, 2006.
A. Bentkamp, Expressiveness of deep learning. Archive of Formal Proofs. 2016. http://isa-afp.org/entries/Deep_Learning.shtml
A. Bentkamp, An Isabelle formalization of the expressiveness of deep learning. 2016. http://matryoshka.gforge.inria.fr/pubs/bentkamp_msc_thesis.pdf
A. Church, “A formulation of the simple theory of types,” J. Symb. Log. vol. 5, no. 2, pp. 56–68, 1940.
N. Cohen, O. Sharir, and A. Shashua, “Deep SimNets,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016.
N. Cohen, O. Sharir, and A. Shashua, “On the expressive power of deep learning: A tensor analysis,” arXiv [cs.NE], 2015)
N. Cohen and A. Shashua, “Convolutional rectifier networks as generalized tensor decompositions,” arXiv [cs.NE], 2016.
N. Cohen, A. Shashua, “Inductive bias of deep convolutional networks through pooling geometry,” CoRR arXiv:1605.06743, 2016.
N. Cohen, R. Tamari, A. Shashua A, “Boosting dilated convolutional networks with mixed tensor decompositions,” CoRR arXiv: 1703.06846, 2017.
M. J. C. Gordon, R. Milner, and C. P. Wadsworth, “Edinburgh LCF: A Mechanised Logic of Computation,” LNCS, vol. 78, 1979.
F. Haftmann, A. Lochbihler, and W. Schreiner, “Towards abstract and executable multivariate polynomials in Isa-belle,” in Isabelle Workshop, T. Nipkow, L. Paulson, and M. Wenzel, Eds. 2014.
J. Hölzl and A. Heller, “Three chapters of measure theory in Isabelle/HOL,” in Interactive Theorem Proving, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 135–151, 2011.
F. Immler and A. Maletzky, “Formal proof development,” in Gröbner bases theory. Archive of Formal Proofs, 2016. http://isa-afp.org/entries/Groebner_Bases.shtml
R. Kam, Case studies in proof checking. 2007. http:// scholar-works.sjsu.edu/cgi/viewcontent.cgi?context=etd_projects&article=1149
K. Kawaguchi, “Deep learning without poor local minima,” arXiv [stat.ML], 2016.
L. Liu, V. Aravantinos, O. Hasan, and S. Tahar, “On the formal analysis of HMM using theorem proving,” in Formal Methods and Software Engineering, Cham: Springer International Publishing, pp. 316–331, 2014.
M. Lotz, “On the volume of tubular neighborhoods of real algebraic varieties,” Proc. Am. Math. Soc. vol. 143, no. 5, pp. 1875–1889, 2015.
C. Murphy, P. Gray, and G. Stewart, “Verified perceptron convergence theorem,” in Proceedings of the 1st ACM SIGPLAN International Workshop on Machine Learning and Programming Languages, pp. 43-50, 2017
T. Nipkow and G. Klein, Concrete Semantics: With Isabelle/HOL. Berlin: Springer, 2014.
T. Nipkow, L. C. Paulson, and M. Wenzel, Isabelle/HOL: A Proof Assistant for Higher-Order Logic, vol. 2283. Berlin: Springer, 2002.
L. Paulson, “Three years of experience with sledgehammer, a practical link between automatic and interactive the-orem provers,” 2018.
L. C. Paulson and K. W. Susanto, “Source-level proof reconstruction for interactive theorem proving,” in Lecture Notes in Computer Science, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 232–245, 2007.
H. Poon and P. Domingos, “Sum-product networks: A new deep architecture,” in 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), 2011.
T. V. H. Prathamesh, Tensor product of matrices. Archive of Formal Proofs. 2016. http://isa-afp. org/entries/Matrix_Tensor.shtml, Formal proof development
D. Selsam, P. Liang, and D. L. Dill, “Developing bug-free machine learning systems with formal mathematics,” arXiv [cs.SE], 2017.
C. Sternagel and R. Thiemann, Executable multivariate polynomials. Archive of Formal Proofs. 2010. http://isa-afp.org/entries/Polynomials.shtml, Formal proof development.
R. Thiemann and A. Yamada, Matrices, Jordan normal forms, and spectral radius theory. Archive of Formal Proofs. 2015. http://isa-afp.org/entries/Jordan_Normal_Form.shtml, Formal proof development.
N. Tishby and N. Zaslavsky, “Deep learning and the information bottleneck principle,” in 2015 IEEE Information Theory Workshop (ITW), 2015.
M. Wenzel, “Isar-A generic interpretative approach to readable formal proof documents,” in Theorem Proving in Higher Order Logic (TPHOLs ’99), vol. 1690, Y. Bertot, G. Dowek, A. Hirschowitz, C. Paulin-Mohring, and L. Théry, Eds. Springer, pp. 167–184, 1999.
S. Rizvi and C. Singh, “Hausdorff Measures in Caratheodary Construction, Vital Covering Theorem,” in Steiner Symmetrization & Isodiametric Inequality"ICTSGA-1, Taylor and Francis ISC2022: CRC Press, pp. 6–34.
S. Rizvi and C. Singh, “Disital point for Borel Measure,” vol. 12, 2024
S. Rizvi and C. Singh, “ON EXISTENCE OF THE SUPPORT OF A BOREL MEASURE AND THEIR REMARKABLE PROPERTIES,” vol. 11, 2024.
Downloads
Published
How to Cite
CITATION COUNT
Issue
Section
License
Copyright (c) 2025 Sakina Rizvi, Dr. Chitra Singh

This work is licensed under a Creative Commons Attribution 4.0 International License.



























