M - projective curvature tensor equipped with an ϵ-kenmotsu manifold

DOI:
https://doi.org/10.54060/a2zjournals.jase.103Keywords:
Trans Sasakian manifold, ϵ- Kenmotsu manifold, M -projective curvature tensor, Einstein manifoldAbstract
In this paper, we studied the properties of ϵ-Kenmotsu manifolds that posses an M -projective curvature tensor. We have shown that ϵ-Kenmotsu manifolds with an M -projectively flat and irrotational M -projective curvature tensor are locally isometric to the hyperbolic space Hn(c), where c = −ϵ2. Additionally, we have investigate the condition R(X, Y ) · S = 0 for M -projectively flat ϵ-Kenmotsu manifolds. Then we focused on the analysis of ϵ-Kenmotsu manifolds with a conservative M -projective curvature tensor. Lastly, we have certain geometric results for ϵ-Kenmotsu manifolds that satisfy the relation M (X, Y ) · R = 0.
Downloads
References
Bejancu, “Real hypersurfaces of indefinite K¨ahler manifolds,” Pacific J. Math, vol. 16, pp. 545–556, 1993.
“Blaga: η-Ricci solitons on para-Kenmotsu manifolds,” Balkan J. Geom. Applicat, vol. 20, pp. 1–13, 2015.
U. C. De and A. Sarkar, “On ϵ-Kenmotsu manifold,” Hardonic J, vol. 32, pp. 231–242, 2009.
K. L. Duggal and R. Sharma, Symmetries of space time and Riemannian manifolds. Kluwer Acad. Publishers, 1999.
L. P. Eisenhart, “Symmetric tensor of the second order whose first covariant derivatives are zero,” Tran. Amer. Math. Soc. vol. 25, pp. 297-306, 1923.
A. Haseeb, “De: η-Ricci solitions in ϵ-Kenmotsu manifolds,” J. Geom, vol. 110, pp. 1–12, 2019.
A. Haseeb, M. K. Khan, and M. D. Siddiqi, “Some more results on an ϵ-Kenmotsu manifold with a semi-symmetric metric connenction,” Acta. Math. Univ. Comenianae, LXXXV, pp. 9–20, 2016.
A. Haseeb, “Some results on projective curvature tensor in an ϵ-Kenmotsu manifold,” Palestine J. Math, vol. 6, pp. 196–203, 2017.
K. Kenmotsu, “A class of almost contact Riemannian manifolds,” Tohoku Math. J. (2), vol. 24, no. 1, pp. 93–103, 1972.
R. N. Sing, S. K. Pandey, G. Pandey, and K. Tiwari, “On a semi-symmetric metric connention in an ϵ-Kenmotsu manifold,” Commun. Korean Math. Soc, vol. 29, pp. 331–343, 2014.
V. Venkatesha, “Vishnuvardhana: ϵ-Kenmotsu manifolds admiting a semi-symmetric connection,” Italian J. Pure Appl. Math, vol. 38, pp. 615–623, 2017.
X. Xufeng and C. Xiaoli, “Two therems on ϵ-Sasakian manifolds,” Internat. J. Math. Math Sci, vol. 21, pp. 249–254, 1998.
C. S. Bagewadi and E. Kumar, Notes on trans-Sasakian manifolds, vol. 65. Tensor N.S, 2004.
C. L. Bejan and M. Crasmareanu, “Second order parallel tensors and Ricci solitons in 3 - dimen- sional normal paracontact geometry,” Anal. Global Anal.Geom, vol. 46, no. 2, pp. 117–127, 2014.
D. E. Blair, “Contact manifolds in Riemannian geometry,” 1976.
S. K. Chaubey and R. H. Ojha, “On the M - projective curvature tensor of a Kenmotsu manifold,” Differ. Geom. Dyn. Syst, vol. 12, pp. 52–60, 2010.
U. C. De and A. Sarkar, “On ϵ-Kenmotsu manifolds,” Hardonic J, vol. 32, pp. 231–242, 2009.
A. Yıldız, U. C. De, and B. E. Acet, “On Kenmotsu manifolds satisfying certain curvature conditions,” SUT J. Math., vol. 45, no. 2, 2009.
U. C. De, S. Mallick, “Space times admitting M - projective curvature tensor,” Bulg. J. Phys., vol. 39, pp. 331-338, 2012.
A. Gray and L. M. Hervella, “The sixteen classes of almost Hermitian man-ifolds and their linear invariants,” Ann. Mat. Pura Appl, vol. 123, no. 1, pp. 35–58, 1980.
G. Ingalahalli and C. S. Bagewadi, “Ricci solitons in α-Sasakian manifolds,” ISRN Geom., vol. 2012, pp. 1–13, 2012.
I. Mahai, R. Rosca, and P.-S. On Lorentzian, Classical Anal-ysis, World Scien- tific Pable. Singapore, 1992.
J. C. Marrero, “The local structure of trans-Sasakian manifolds,” Ann. Mat. Pura Appl. (4), vol. 162, no. 1, pp. 77–86, 1992.
K. Matsumoto, “On Lorentzian para contact manifolds,” Bull. Yamagata Univ.Natur. Sci, vol. 12, pp. 151–156, 1989.
R. S. Mishra, Almost contact metric manifolds, vol. 1. Lucknow: Tensor Societyof India, 1991.
R. H. Ojha, “M - projectively flat Sasakian manifolds,” Indian J. Pure Appl.Math, vol. 17, pp. 481–484, 1986.
G. P. Pokhariyal, R. S. and Mishra, “Curvature tensors and their relativistic signification II,” Yoko- hama Math. J.,vol. 18, pp. 105-108, 1970.
A. Prakash, M. Ahmad, and A. Srivastava, “M - projective curvature tensoron a Lorentzian para-Sasakian manifolds,” IOSR-JM, vol. 6, no. 1, pp. 19–23, 2013.
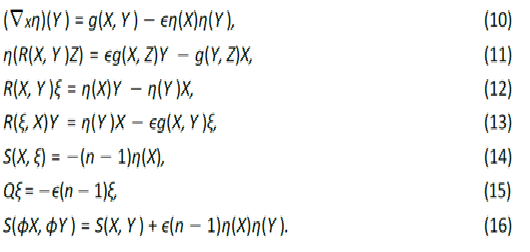
Downloads
Published
How to Cite
CITATION COUNT
Issue
Section
License
Copyright (c) 2025 N.V.C.Shukla, Mantasha

This work is licensed under a Creative Commons Attribution 4.0 International License.



























