Summation Formulae Associated with the Extension of Voigt Function and Bessel-Maitland Function and Its Applications

DOI:
https://doi.org/10.54060/a2zjournals.jase.107Keywords:
Voigt function, H-function of two variable, Laguerre polynomial, generating functionAbstract
In this paper we establish a series expansion formula which involving Laguerre polynomial and extension of Voigt function in terms of H-function of two variable, by making use of an interesting generating function for Laguerre polynomial. For the sake of illustration, we obtain some special cases of our main results which are interesting and believed to be new.
Downloads
References
P. Appell and L. Sur, “Series Hypergéometriqués de Duex Variables,” in et Sur des Equations, Dif-fren-tiellesLinearies aux DeriveesPartielles, CR Acad. Sci, vol. 90, pp. 296–298, Paris, 1880.
P. Appell and J. Kampé De Fériet, Functions Hypergéométriques et HypersphériquesPo-lynômesd’ Hermite. Gauthier-Villars Paris, 1926.
S. P. Goyal, “The H-function of two variables, Kyungpook-Math,” J. Vol. 15, pp. 117-131, 1975.
S. P. Goyal and R. Mukherjee, “Generalizations of the Voigt functions through generalized Lau-ricella func-tion,” GanitaSandesh, vol. 13, no. 1, pp. 31–41, 1999.
K. C. Gupta and A. Gupta, “On the study of unified representations of the generalized Voigt func-tions,” Palestine J. Math, vol. 2, no. 1, pp. 32–37, 2013.
K. C. Gupta, S. P. Goyal, and R. Mukherjee, “Some results on generalized Voigt functions,” ANZIAM J, vol. 44, pp. 299–303, 2002.
R. Jain and B. Bundela, “Summation formula involving generalized Voigt functions, Pseudo La-guerre Polynomial and Parabolic Cylinder Function,” Ganita Sandesh, vol. 24, no. 1, pp. 47–54, 2010.
J. Kampé De Fériet, “functions Hypergéométriq uesd’ordresuperieur or deluxe variables,” vol. 173, pp. 401–404, 1921.
N. Khan, M. Ghayasuddin, W. A. Khan, T. Abdeljawad, and S. Nisar, Further exten-sion of Voigt function and its propertie. Springer, 2020.
N. U. Khan, M. Kamarujjama, and M. Ghayasuddin, “A generalization of Voigt function involving generalized Whittaker and Bessel functions,” Palestine J. Math, vol. 4, no. 2, pp. 313–318, 2015.
M. A. Pathan, K. Gupta, and V. Agrawal, “Summation formulae involving Voigt functions and generalized hy-pergeometric functions,” Scientia, Ser. A, Math. Sci, vol. 19, pp. 37–44, 2010.
M. A. Pathan, M. Garg, and S. Mittal, “On unified presentations of the multivariable Voigt functions,” East-West J. Math, vol. 8, no. 1, pp. 49–59, 2006.
M. A. Pathan and M. J. S. Shahwan, “New representations of the Voigt functions,” Demonstratio Math., vol. 39, no. 1, pp. 75–80, 2006.
A. E. Danese and E. D. Rainville, “Special Functions,” Am. Math. Mon., vol. 67, no. 10, p. 1044, 1960.
R. L. Shively, On Pseudo Laguerre polynomials. 1953.
H. M. Srivastava and M.-P. Chen, “Some unified presentations of the Voigt functions,” Astrophys. Space Sci., vol. 192, no. 1, pp. 63–74, 1992.
H. M. Srivastava, K. C. Gupta, and S. P. Goyal, The H-Functions of One and Two Variables with Applications. New Delhi and Madras: South Asian Publishers, 1982.
H. M. Srivastava and C. M. Joshi, “Integration of certain products associated with a generalized Meijer func-tion,” Math. Proc. Camb. Philos. Soc., vol. 65, no. 2, pp. 471–477, 1969.
H. M. Srivastava and P. W. Karlson, Multiple Gaussian Hypergeometric Series. John Wiley and Sons Inc, 1985.
H. M. Srivastava and E. A. Miller, “A unified presentation of the Voigt functions,” Astrophys. Space Sci., vol. 135, no. 1, pp. 111–118, 1987.
H. M. Srivastava, M. A. Pathan, and M. Kamarujjama, “Some unified presentations of the generalized Voigt functions,” Commun. Appl. Anal, vol. 2, pp. 49–64, 1998
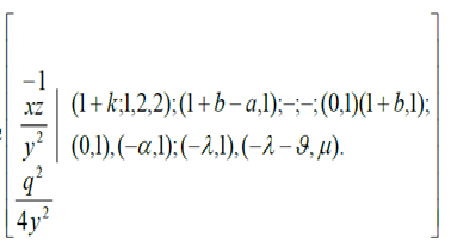
Downloads
Published
How to Cite
CITATION COUNT
Issue
Section
License
Copyright (c) 2025 Swati Domaji Kharabe, Beena Bundela, Manish Kumar Bansal, Deepak Gupta

This work is licensed under a Creative Commons Attribution 4.0 International License.



























