Mathematical Modelling Based on Runge-Kutta Method

Abstract

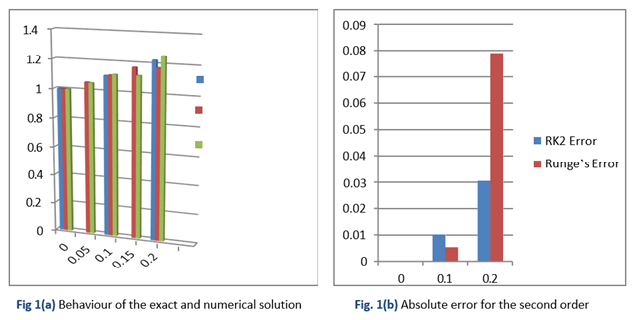
In this research paper, the Runge-Kutta method is used to minimize the error estimation in solving the problem of ordinary differential equations. By using the Runge-Kutta method, we can construct a higher- order accurate functions without having to calculate higher-order derivatives. The results show that the minimum error is obtained by using the Runge-Kutta second, third, and fourth order methods with step doubling method. It is important to note that there exists a straightforward technique for adaptive step size control in fourth-order Runge-Kutta, known as the step-doubling method (also referred to as the Local Error method). The method estimates the error by taking two steps of half the size and comparing the results. The computational simplicity of the step-doubling technique is an advantage, but in practice, algorithms based on embedded Runge-Kutta formulas are found to be more efficient.