Understanding Covid-19 Situation Using Mathematical Modeling
English

DOI:
https://doi.org/10.54060/jase.2023.41Keywords:
Covid-19, Mathematical Modeling, Susceptible Exposed Infected Recovered (SEIR)Abstract
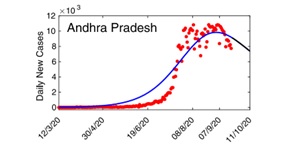
In light of the absence of an effective vaccine or specific antiviral treatments, mathematical modeling assumes a crucial role in enhancing our comprehension of disease dynamics and in devising strategies to manage the rapid spread of infectious diseases. Particularly during this period, forecasting holds paramount significance for healthcare planning and for effectively addressing the COVID-19 pandemic. To eluci-date the dynamics of the COVID-19 outbreak, this study introduces an extended SEIR compartment model, refined with the inclusion of contact tracing and hospitalization strategies. The model is calibrated employing daily COVID-19 data encompassing various Indian regions, including Kerala, Karnataka, Andhra Pradesh, Maharashtra, West Bengal, and the entirety of India. Employing the least squares method, we es-timate sensitive parameters after conducting a sensitivity analysis, which we ap-proach using partial rank correlation coefficient techniques. Our exploration focuses on the relative significance of system parameters, with a dedicated sensitivity analy-sis centered on the reproductive number R₀. To assess the model's resilience across parameter variations, we compute R₀ sensitivity indices. Our findings underscore the effectiveness of strategies that involve reducing disease transmission coefficients (s) and clinical outbreak rates (qa) in controlling COVID-19 outbreaks. Our study gener-ates short-term predictions for daily and cumulative confirmed COVID-19 cases across the five Indian provinces. These projections reveal distinct trends, with certain states demonstrating steady exponential growth, while others exhibit a decline in daily new cases. Examining the long-term perspective, our model predicts oscillatory dynamics for COVID-19 cases in India, suggesting the potential for the disease to follow a seasonal pattern. Consequently, our simulation points towards a power law trend in coronavirus cases in India by the close of September 2020, further contrib-uting to our understanding of the disease's progression.
Downloads
References
I. Aldawish & R. W. Ibrahim, “A new mathematical model of multi-faced COVID-19 formulated by fractional derivative chains,” Adv. Contin. Discrete Model, vol.2022, no.6, 2022.
N. Zhu, D. Zhang, W. Wang, et al., “A novel Coronavirus from patients with pneumonia in China 2019,” N. Engl. J. Med., vol.382, no.8, pp.727–733, 2020.
J. F.W. Chan, S. Yuan, K. H. Kok, et al., “A familial cluster of pneumonia associated with the 2019 novel coronavirus indi-cating person-to-person transmission: a study of a family cluster,” Lancet, vol.395, no. 10223, pp.514–523, 2020.
J. Cohen & D. Normile, “New SARS-like virus in China triggers alarm,” Science, vol.367, no.6475, pp.234–235, 2020.
A. K. Pandey & T. Srivastava, “Mathematical Modelling: Growing Role and Applications”, J. Appl. Sci. Educ., vol.1, no.1, pp.1–11, Nov 2021.
A. B. Gumel, S. Ruan, T. Day, et al., “Modelling strategies for controlling SARS outbreaks,” Proc. Biol. Sci., vol.271, no.1554, pp.2223–2232, 2004.
C. Drosten, S. Guntur, W. Preiser, et al., “Identification of a novel coronavirus in patients with severe acute respiratory syndrome,” N. Engl. J. Med., vol.348, no.20, pp.1967–1976, 2003.
P. Zhou, X. L. Yang, B. Heu, et al., “A pneumonia outbreak associated with a new coronavirus of probable bat origin,” Nature, vol.579, pp. 270–273, 2020.
P. Zhou, X. L. Yang, B. Heu, et al., “Addendum: A pneumonia outbreak associated with a new coronavirus of probable bat origin,” Nature, vol.588, no. E6, 2020.
J. Wang, K. Tang, K. Feng, et al., “High temperature and high humidity reduce the transmission of COVID-19,” SSRN Elec-tron. J., 2020.
S. K. Biswas, J. K. Ghosh, S. Sarkar, et al., “COVID-19 pandemic in India: a mathematical model study,” Nonlinear Dyn, vol.102, no.1, pp.537–553, 2020.
N. Sharma, P. S. Rana, and S. S. Negi, “Mathematical modeling and case study analysis for COVID-19 pandemic in India,” in AIP Conference Proceedings, vol.2435, no.1, 2022.
A. De Fina and S. M. Perrino, “Chronotopes and the COVID-19 pandemic,” Language, Culture and Society, vol.4, no.2, pp.98–109, 2022.
L. Wang, M. Y. Li, and D. Kirschner, “Mathematical analysis of the global dynamics of a model for HTLV-I infection and ATL progression,” Math. Biosci., vol.179, no.2, pp.207–217, 2002.
R. M. Anderson, H. Heesterbeek, D. Klinkenberg, et al., “How will country-based mitigation measures influence the course of the COVID-19 epidemic,” Lancet, vol.395, no.10228, pp.931–934, 2020.
M. Egger, L. Johnson, C. Althaus, et al., “Developing WHO guidelines: Time to formally include evidence from mathemati-cal modelling studies,” F1000Res., vol.6, no.1584, 2017.
Downloads
Published
How to Cite
CITATION COUNT
Issue
Section
License
Copyright (c) 2023 Samkach Singh, Ambrish Pandey

This work is licensed under a Creative Commons Attribution 4.0 International License.



























